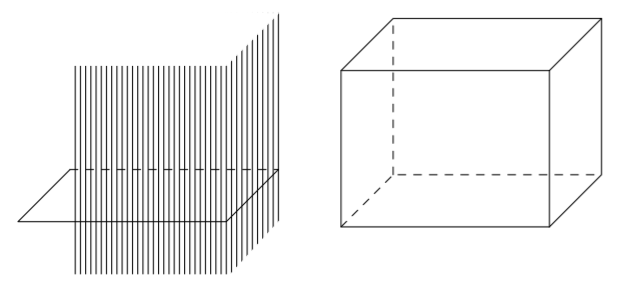
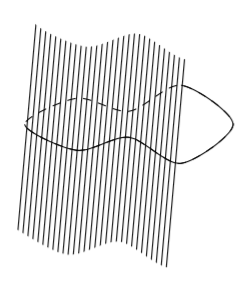
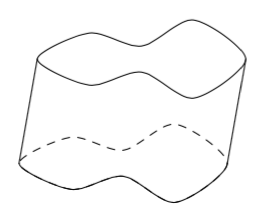
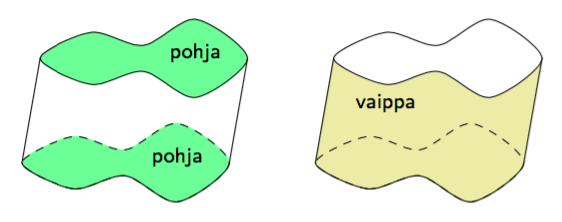
Tässä kappaleessa tutkitaan ympyrän geometrisia ominaisuuksia. Aloitetaan määrittelemällä, mitä tarkoitetaan ympyrällä ja joillakin siihen liittyvillä käsitteillä.
MÄÄRITELMÄ: YMPYRÄ
Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen säde.
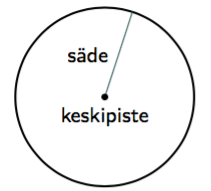
Jänne on ympyrän kahden pisteen välinen jana. Halkaisija on ympyrän keskipisteen kautta kulkeva jänne.
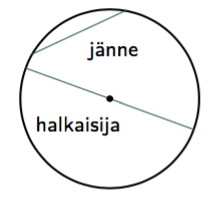
Nimitystä ympyrä käytetään toisinaan myös ympyräviivan sisään jäävästä tasoalueesta. Ympyräviivaa itseään kutsutaan tällöin usein ympyrän kehäksi.
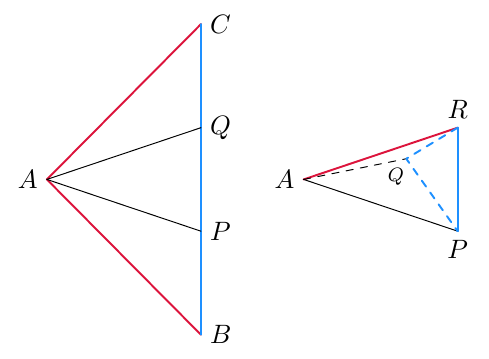
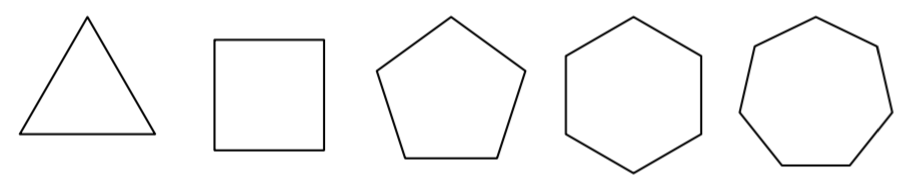
Ympyrän kehän pituutta voidaan arvioida säännöllisten monikulmioiden avulla piirtämällä monikulmiot sekä ympyrän sisä- että ulkopuolelle alla olevien kuvien mukaisesti. Mitä enemmän kulmia monikulmioissa on, sitä tarkemmin niiden piirit arvioivat ympyrän kehän pituutta.
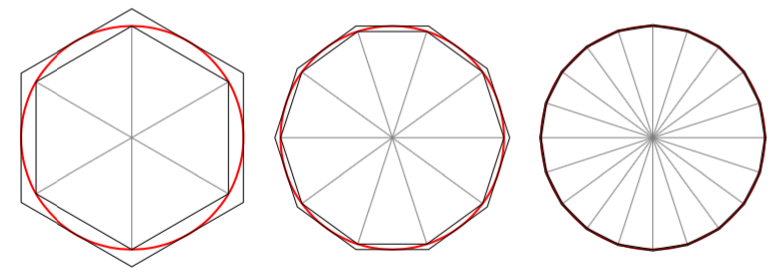
Tällä tavalla voidaan arvioida myös ympyrän kehän pituuden suhdetta ympyrän halkaisijaan. Tämä suhde ei riipu ympyrän koosta vaan on sama kaikilla ympyröillä. Kysymyksessä onkin yksi kuuluisimmista matemaattisista vakioista. Sitä merkitään kirjaimella $\pi$ (pii).
MÄÄRITELMÄ: LUKU $\pi$
Luku $\pi$ on ympyrän kehän pituuden $p$ suhde halkaisijan pituuteen $d$: $$\pi = \frac{p}{d}$$ 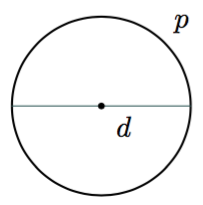
Luku $\pi$ on irrationaaliluku, eli sitä ei voi kirjoittaa murtolukumuodossa. Tästä seuraa, että ympyrän kehän pituus $p$ ja halkaisija $d$ eivät voi olla yhtä aikaa rationaalilukuja, vaan ainakin toinen niistä on aina irrationaalinen.
Luvun $\pi$ viisidesimaalinen likiarvo on $3{,}14159$. Vuonna 2013 Alexander Yee ja Shigeru Kondo selvittivät tietokoneen avulla likiarvon yli 12,1 biljoonan desimaalin tarkkuudella (12 100 000 000 050 ensimmäistä desimaalia).
Tässä tehtävässä käytetään luvun $\pi$ määritelmää ympyrän kehän pituuden selvittämiseen.
- Ympyrän halkaisija on 15,0 cm. Laske sen kehän pituus ja anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Muodosta yhtälö, jonka avulla saat laskettua ympyrän kehän pituuden $p$, jos tiedät ympyrän säteen $r$.
- Kehän pituus on noin 47,1 cm.
- $p = 2\pi r$
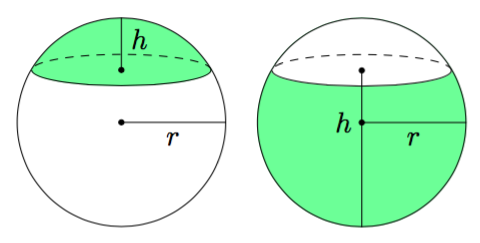
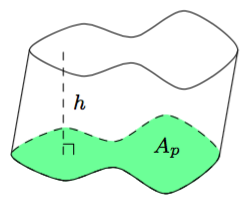
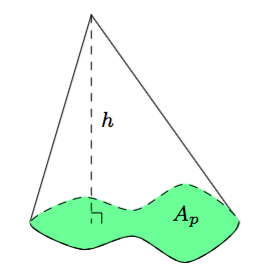
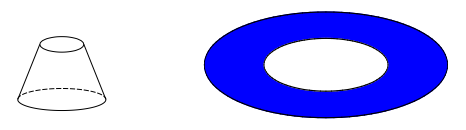
Ympyrän pinta-alaa voidaan arvioida monin tavoin. Yksi mahdollisuus on piirtää säännölliset monikulmiot sekä ympyrän sisä- että ulkopuolelle samaan tapaan kuin kehän pituutta arvoidessa. Seuraavassa tehtävässä tutustutaan toisenlaiseen tapaan järkeillä ympyrän pinta-ala.
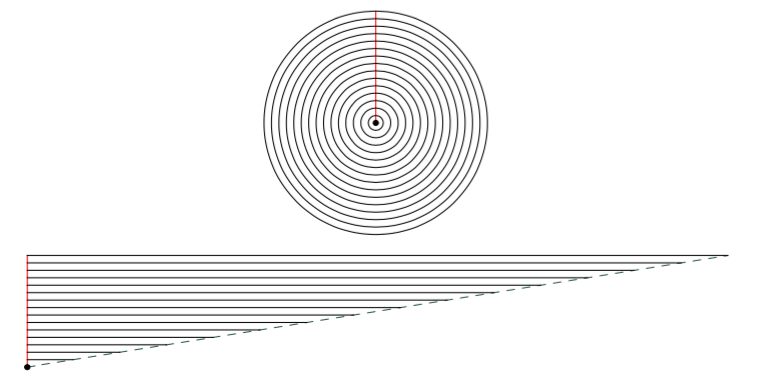
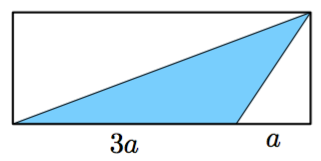
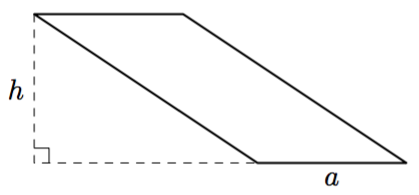
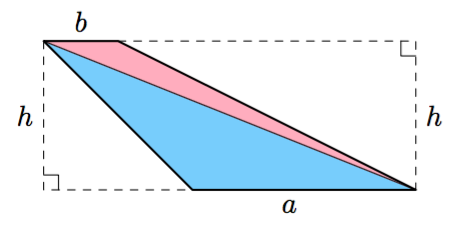
Yllä olevassa kuvassa ympyrä on jaettu ohuisiin ympyrärenkaan muotoisiin osiin. Kun ympyrä leikataan punaista viivaa pitkin ja jokainen ohut ympyrärengas taivutetaan auki, muodostuu kuvassa näkyvä kolmion muotoinen kuvio.
- Mikä on ympyrän kehän pituus, jos ympyrän säde on $r$?
Vinkki: tehtävä 2.19. - Ilmaise yllä olevan kolmion kanta ja korkeus alkuperäisen ympyrän säteen $r$ avulla.
- Muodosta lauseke kolmion pinta-alalle. Miten se liittyy alkuperäisen ympyrän pinta-alaan? Selitä omin sanoin.
Tehtävien 2.19 ja 2.20 tuloksista saadaan seuraava teoreema:
TEOREEMA
Ympyrän pinta-ala $A$ ja kehän pituus $p$ riippuvat ympyrän säteestä $r$ seuraavasti: \begin{align*} A &= \pi r^2 \\ p &= 2\pi r \end{align*}
Perustelu: tehtävissä 2.19 ja 2.20.
Käytettävissä on rakennustarvikkeet 80 metrin aitaa varten. Tehtävänä on selvittää, kannattaako aitauksesta rakentaa ympyrän vai neliön muotoinen, jos aitauksen pinta-alan halutaan olevan mahdollisimman suuri. Lisäksi pitää selvittää, kuinka iso ero näillä kahdella vaihtoehdolla on.
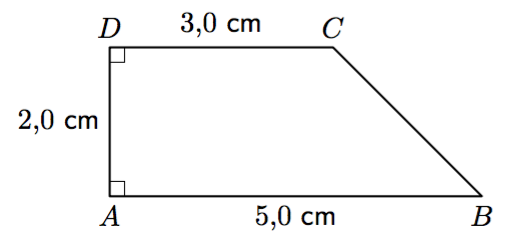
- Piirrä kummastakin vaihtoehdosta mallikuva ja merkitse siihen tunnetut tai helposti pääteltävissä olevat mitat.
- Kuinka suuri on 80 metriä pitkällä aidalla aidatun neliön muotoisen alueen pinta-ala?
- Kuinka suuri on 80 metriä pitkällä aidalla aidatun ympyrän muotoisen alueen pinta-ala?
- Kuinka monta prosenttia isomman alueen pinta-ala on suurempi kuin pienemmän alueen pinta-ala?
-
- $400 \text{ m}^2$
- Noin $509 \text{ m}^2$.
- Noin 27,3 %.
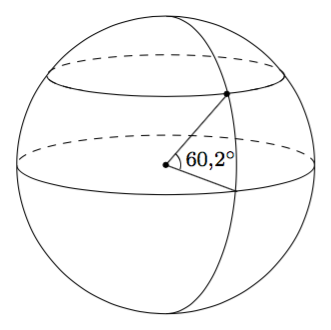
Siirrytään nyt tutkimaan erilaisia ympyrän osia. Aloitetaan määrittelemällä, mitä tarkoitetaan ympryrän keskuskulmalla.
MÄÄRITELMÄ: KESKUSKULMA
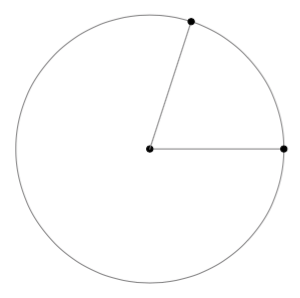
Kulma, jonka kärki on ympyrän keskipisteessä, on keskuskulma.
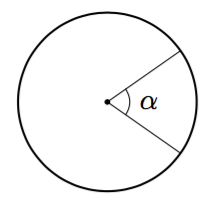
Keskuskulman suuruus voi olla mitä tahansa nollakulman ja täyden kulman väliltä.
Keskuskulman avulla määritellään kaaren ja sektorin käsitteet:
MÄÄRITELMÄ: KAARI, SEKTORI JA SEGMENTTI
Keskuskulman kyljet rajaavat ympyrän kehältä kaaren ja ympyrän sisältä sektorin.
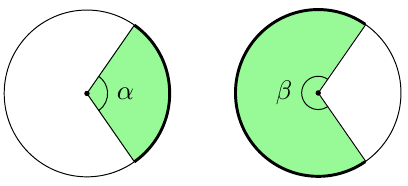
Kaari ja sen päätepisteitä yhdistävä jänne rajaavat ympyrän sisältä segmentin.

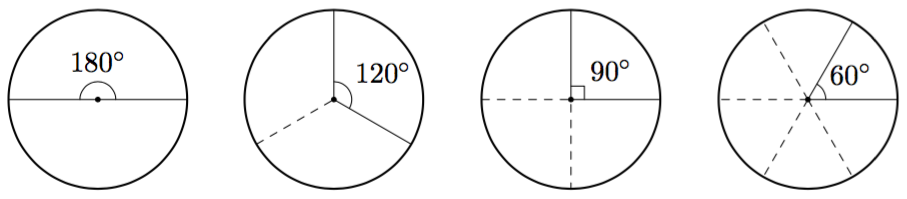
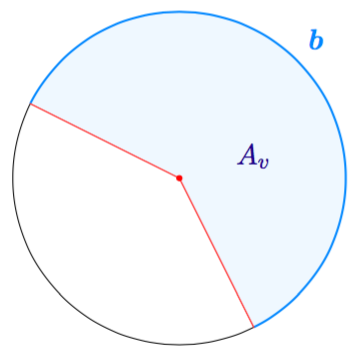
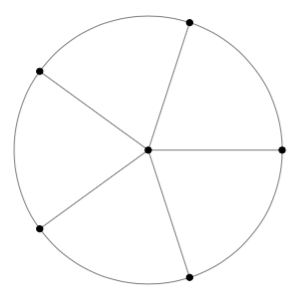
Alla olevassa taulukossa on lueteltu joitakin ympyrän keskuskulmia $\alpha$. Piirrä vastaava taulukko vihkoosi ja täydennä siihen puuttuvat tiedot: keskuskulman suhde täyteen kulmaan (supistetussa murtolukumuodossa) sekä keskuskulmaa vastaava kaaren osuus ympyrän kehästä ja keskuskulmaa vastaavan sektorin osuus ympyrän pinta-alasta. Voit käyttää päättelyssä apuna esimerkiksi yllä olevaa kuvaa.
| $\alpha$ | $\dfrac{\alpha}{360^\circ}$ | Kaaren osuus ympyrän kehästä | Sektorin osuus ympyrän pinta-alasta |
| $180^\circ$ | | | |
| $120^\circ$ | | | |
| $\phantom{1}90^\circ$ | | | |
| $\phantom{1}60^\circ$ | | | |
| $\phantom{1}45^\circ$ | | | |
| $\phantom{1}36^\circ$ | | | |
| $\phantom{1}30^\circ$ | | | |
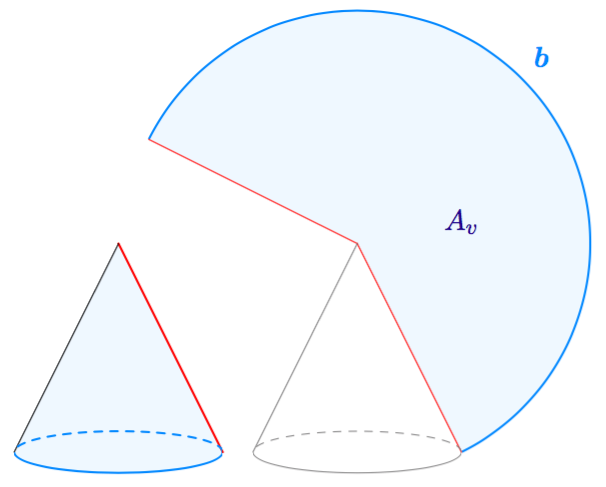
Tehtävässä 2.22 havaittiin, että ympyrän kaaren pituus ja sektorin pinta-ala voidaan päätellä laskemalla niitä vastaavan keskuskulman $\alpha$ suhde täyskulmaan eli $$\frac{\alpha}{360^\circ}$$ ja ottamalla tämän suhteen mukainen osuus ympyrän kehän pituudesta ja ympyrän pinta-alasta. Tämä havainto johtaa seuraavaan teoreemaan, jonka yksityiskohtaisempi perustelu sivuutetaan.
TEOREEMA
Kaaren pituus $b$ ja sektorin pinta-ala $A_S$ riippuvat keskuskulmasta $\alpha$ ja ympyrän säteestä $r$ seuraavasti: \begin{align*} b &= \dfrac{\alpha}{360^\circ} \cdot 2\pi r \\[1mm] A_S &= \dfrac{\alpha}{360^\circ} \cdot \pi r^2 \end{align*}
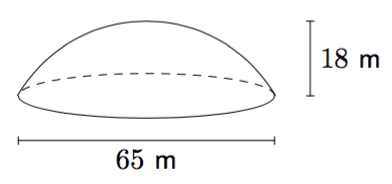
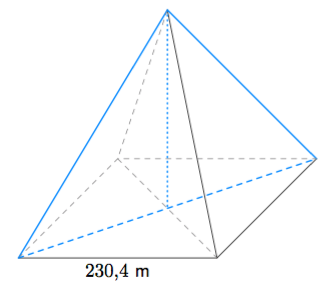
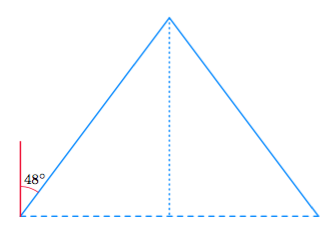
Alla on kuvattu yleisurheilukentän juoksuratojen sisäpuolinen alue. Päädyt ovat puoliympyrän muotoiset. Kaarteen pituus on 115,61 metriä.
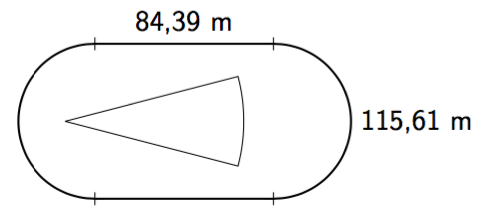
Tehtävänä on selvittää, miten suuri osuus tästä alueesta on varattava keihäänheiton alastuloalueelle. Suositusten mukaan keihäänheiton alastuloalueen pituus on kansainvälisissä kilpailuissa 105 metriä. Heittosektorin keskuskulman suuruus on $29^\circ$.
- Laske juoksuratojen sisäpuolisen alueen pinta-ala.
Vinkki: Aloita selvittämällä päädyn puoliympyrän säde. - Laske keihäänheiton heittosektorin pinta-ala. Kuinka monta prosenttia se on juoksuratojen sisäpuolisen alueen pinta-alasta?
- Pinta-ala on noin $10\,465 \text{ m}^2$. (Päädyn puoliympyrän säde on noin 36,80 m.)
- Heittosektorin pinta-ala on noin $2\,790 \text{ m}^2$. Se on noin 26,7 % juoksuratojen sisäpuolisen alueen pinta-alasta.
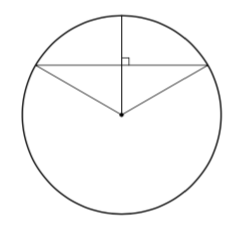
Segmentin pinta-ala saadaan laskettua sektorin pinta-alan sekä säteiden ja jänteen rajaaman niin sanotun keskuskolmion pinta-alan avulla:
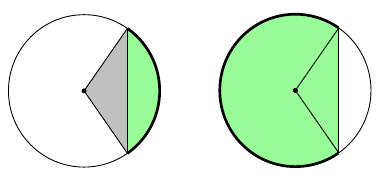
Ympyrän säde on 6. Tehtävänä on määrittää $70^\circ$ keskuskulmaa vastaavan segmentin pinta-ala.
- Piirrä tilanteesta mallikuva harpin ja kolmioviivaimen avulla.
- Laske $70^\circ$ keskuskulmaa vastaavan sektorin pinta-ala.
- Merkitse mallikuvaan kaikki keskuskolmion sivujen pituudet ja kulmat, jotka tiedät tai pystyt päättelemään vähällä vaivalla. Palauta mieleesi, millä eri tavoilla kolmion pinta-alan voi laskea.
Vinkki: teoreemat 1 & 6. - Laske keskuskolmion pinta-ala.
- Laske segmentin pinta-ala.
-
- Sektorin pinta-ala on $7\pi \approx 21{,}99$.
-
- Keskuskolmion pinta-ala on noin 16,91.
- Segmentin pinta-ala on noin 5,08.
New Yorkin ja Los Angelesin välinen etäisyys on linnuntietä noin 3 900 km. Tehtävänä on selvittää, kuinka paljon lyhyempi matka olisi, jos kaupungit yhdistettäisiin suoralla tunnelilla. Maapallon säde on noin 6 370 km.
- Piirrä tilanteesta mallikuva (maapallon poikkileikkaus) harpin ja kolmioviivaimen avulla. Merkitse kuvaan kaikki tunnetut mitat.
- Laske maapallon ympärysmitta. Selvitä, mikä on New Yorkin ja Los Angelesin välistä etäisyyttä vastaavan keskuskulman suuruus.
- Laske suoran tunnelin pituus. Kuinka paljon matka lyhenisi linnuntiehen verrattuna?
Vinkki: teoreema 8. - Kuinka syvällä maan pinnan alla tunneli kulkisi syvimmässä kohdassaan?
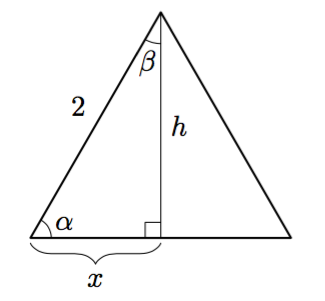
Vinkki: pääset alkuun jakamalla keskuskolmion kahdeksi suorakulmaiseksi kolmioksi ja hyödyntämällä sopivaa trigonometrista suhdetta. - Mitä sanoisit ihmiselle, joka ehdottaa tällaisen tunnelin rakentamista?
-
- Maapallon ympärysmitta on noin 40 000 km ja kysytty keskuskulma noin $35{,}1^\circ$.
- Tunnelin pituus olisi noin 3 840 km, joten matka lyhenisi noin 1,5 %.
- Tunneli kulkisi syvimmillään noin 296 km maanpinnan alapuolella.
-
Ympyrällä ja suoralla voi olla kaksi yhteistä pistettä, yksi yhteinen piste tai ei yhtään yhteistä pistettä. Jos yhteisiä pisteitä on kaksi, jakaa suora ympyrän kahteen segmenttiin. Jos yhteisiä pisteitä on vain yksi, suoraa kutsutaan ympyrän tangentiksi.
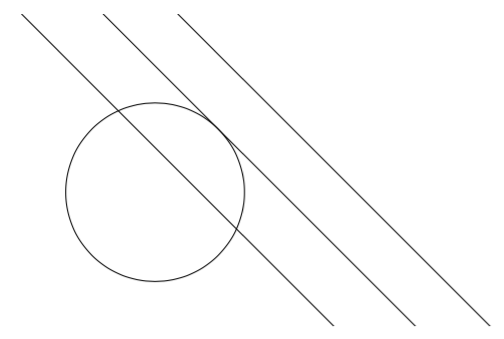
MÄÄRITELMÄ: YMPYRÄN TANGENTTI
Suora, joka kohtaa ympyrän vain yhdessä pisteessä, on ympyrän tangentti.
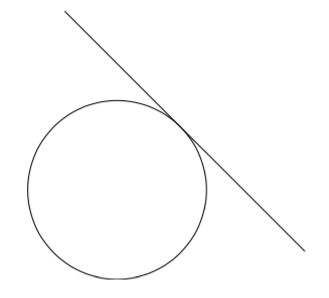
Seuraavassa teoreemassa osoitetaan, että ympyrän tangentti muodostaa aina suoran kulman sivuamispisteeseen piirretyn säteen kanssa. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Ympyrän tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan.
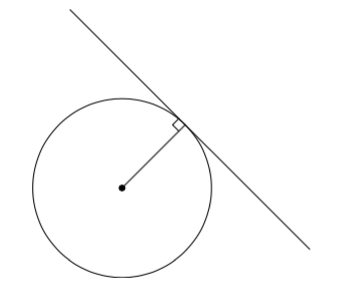
Perustelu: Käytetään niin sanottua epäsuoraa päättelyä: Tutkitaan, mitä seuraa, jos teoreema ei pidäkään paikkaansa. Siis mitä seuraa siitä, jos ympyrän tangentti ei olekaan kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan?
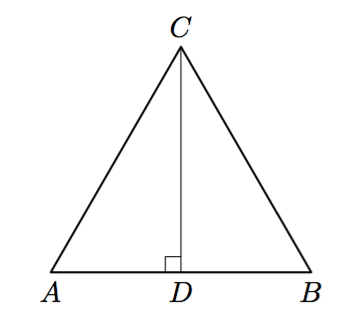
Olkoon ympyrän keskipiste $O$ ja tangentin sivuamispiste $P$. Piirretään ympyrän keskipisteen kautta suora, joka on kohtisuorassa tangenttia vastaan:
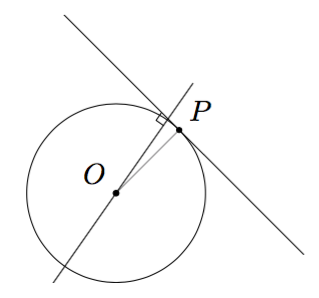
Merkitään tämän suoran ja tangentin leikkauspistettä kirjaimella $Q$. Koska nyt tutkitaan tilannetta, jossa tangentti ja säde $OP$ eivät ole toisiaan vastaan kohtisuorassa, voidaan olla varmoja, että $Q \neq P$.

Tutkitaan tarkemmin kolmiota $OPQ$. Suorat on piirretty niin, että kulma $Q$ on suora kulma. Silloin jana $OP$ on suorakulmaisen kolmion $OPQ$ hypotenuusa. Siten jana $OQ$ on lyhyempi kuin jana $OP$.
Toisaalta piste $Q$ on ympyrän ulkopuolella (vrt. ylempi kuva), joten janan $OQ$ pituus on suurempi kuin ympyrän säde. Janan $OP$ pituus taas on sama kuin ympyrän säde. Siten jana $OQ$ on pitempi kuin jana $OP$.
Näin on päädytty ristiriitaan: jana $OQ$ on yhtä aikaa lyhyempi ja pitempi kuin jana $OP$. Tähän päädyttiin tilanteessa, jossa teoreema ei pitänyt paikkaansa. Voidaan päätellä, että tällainen tilanne on mahdoton. Siis teoreeman täytyy olla tosi.
Seuraavissa tehtävissä harjoitellaan soveltamaan teoreeman 15 tulosta.
Maapallon kaarevan muodon vuoksi kirkkaallakaan säällä ei ole mahdollista nähdä miten tahansa kaukana olevia kohteita, sillä ne jäävät horisontin alapuolelle. Tässä tehtävässä arvioidaan, miten kauas Tallinnan televisiotornista on mahdollista nähdä kirkkaalla säällä.
Tallinnan tv-tornin näköalatasanne ulottuu noin 194 metrin korkeudelle merenpinnasta. Maapallon säde on noin 6 370 km.
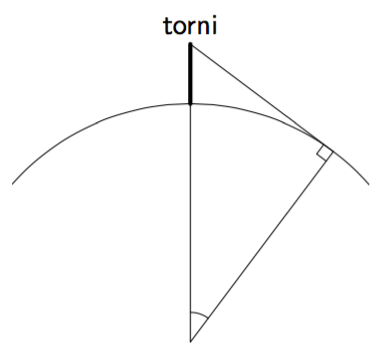
- Yllä on näkyvissä osa maapallon poikkileikkauksesta. Piirrä vihkoosi vastaava mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Selvitä keskuskulman suuruus sopivan trigonometrisen suhteen avulla.
- Laske keskuskulmaa vastaavan kaaren pituus (horisontin etäisyys maanpintaa pitkin). Miten kauas Tallinnan televisiotornista on mahdollista nähdä kirkkaalla säällä?
- Selitä omin sanoin, miten ympyrän tangetti liittyy tähän tehtävään.
-
- Keskuskulma on noin $0{,}447^\circ$.
- Noin 50 km päähän.
-
Kansainvälinen avaruusasema ISS kiertää maapalloa noin 400 km korkeudessa. Tehtävänä on selvittää, missä kulmassa maapallo näkyy avaruusasemalta. Pitää siis määrittää sen kulman suuruus, jonka kärki on avaruusasemalla ja jonka kyljet ovat maapallon poikkileikkausympyrän tangetteja:
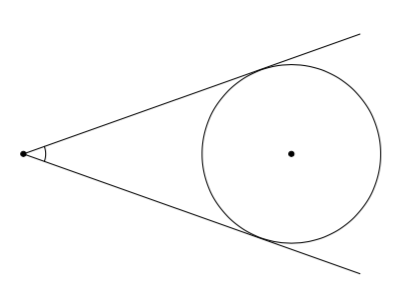
- Piirrä vihkoosi tilanteesta mallikuva kuten yllä. Täydennä kuvaa seuraavasti:
- piirrä jana avaruusasemasta maapallon keskipisteeseen
- piirrä janat maapallon keskipisteestä kummankin tangentin sivuamispisteeseen.
- Merkitse mallikuvaan kaikki tunnetut tai pääteltävissä olevat etäisyydet ja kulmat. Maapallon säde on noin 6370 km.
Vinkki: teoreema 15. - Missä kulmassa maapallo näkyy avaruusasemalta?
Vinkki: selvitä ensin kysytyn kulman puolikas sopivan trigonometrisen suhteen avulla.
-
-
- Noin $140^\circ$ kulmassa.
Jatkoa edelliseen tehtävään. Kansainvälinen avaruusasema ISS kiertää maapalloa noin 400 km korkeudessa. Edellisessä tehtävässä selvitit, missä kulmassa maapallo näkyy avaruusasemalta. Nyt tehtävänä on selvittää, miten kaukana toisistaan kaksi kohdetta maan pinnalla voivat olla, jos ne on mahdollista nähdä avaruusasemalta yhtä aikaa. Pitää siis määrittää tangenttien sivuamispisteiden määräämän kaaren pituus:

- Hyödynnä edellisessä tehtävässä piirtämääsi mallikuvaa ja päättele kaarta vastaavan keskuskulman suuruus.
- Miten kaukana toisistaan kaksi kohdetta maan pinnalla voivat olla, jos ne on mahdollista nähdä avaruusasemalta yhtä aikaa?
Onko avaruusasemalta mahdollista nähdä koko Afrikka yhdessä silmänräpäyksessä? Afrikan läntisimmästä kohdasta Senegalissa on noin 7400 km sen itäisimpään kohtaan Somaliassa.
- Keskuskulma on noin $40^\circ$.
- Avaruusasemalta on mahdollista nähdä yhtä aikaa kohteet, joiden etäisyys on enintään noin 4 400 km. Koko Afrikkaa ei siis ole mahdollista nähdä yhdessä silmänräpäyksessä.
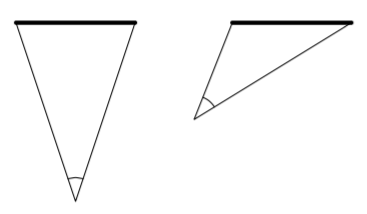
Edellisissä tehtävissä tutkittiin ympyrän ulkopuolella sijaitsevasta pisteestä ympyrälle piirrettyjen tangenttien välistä kulmaa. Tätä kulmaa on tapana kutsua tangenttikulmaksi.
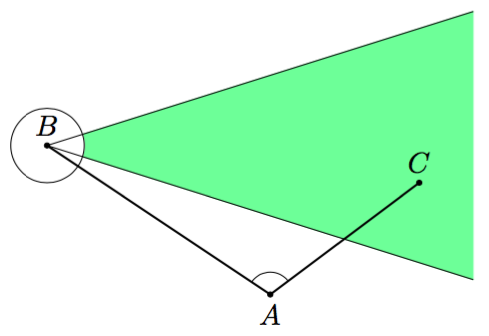
Tangettikulman tarkasssa määritelmässä käytetään kulman aukeaman käsitettä. Kulman aukeama tarkoittaa kulman rajaamaa tason osaa, josta alla olevassa kuvassa on näkyvissä pieni pala:
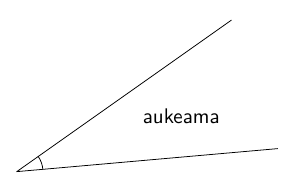
MÄÄRITELMÄ: TANGENTTIKULMA
Ympyrän kahden tangentin leikkauspisteeseen muodostuva kulma, jonka aukeamaan ympyrä sisältyy, on tangenttikulma.
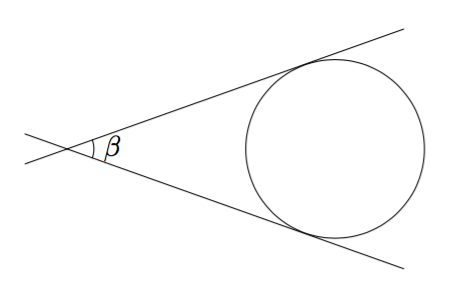
Seuraavassa tehtävässä tutkitaan, miten tangenttikulma ja sitä vastaava keskuskulma liittyvät toisiinsa.
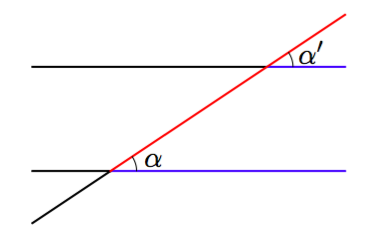
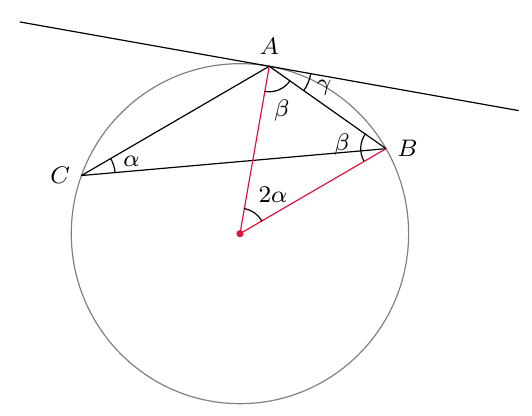
Alla on näkyvissä tangenttikulma ja sitä vastaava keskuskulma. Mitä voit päätellä niiden summasta $\alpha + \beta$?
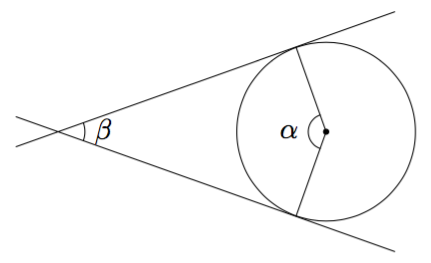
Vinkki: teoreemat 11 & 15.
Tehtävän 2.29 tuloksena saadaan seuraava teoreema:
TEOREEMA
Tangenttikulman ja sitä vastaavan keskuskulman summa on oikokulma.
Perustelu: tehtävässä 2.29.
Aiemmin on sovittu, että keskuskulma tarkoittaa kulmaa, jonka kärki on ympyrän keskipisteessä. Vastaavasti kehäkulma tarkoittaa kulmaa, jonka kärki on ympyrän kehällä. Määritelmässä vaaditaan lisäksi, että kulma on kovera eli suurempi kuin nollakulma ja pienempi kuin oikokulma.
MÄÄRITELMÄ: KEHÄKULMA
Kovera kulma, jonka kärki on ympyrän kehällä ja jonka kyljet ovat ympyrän jänteitä, on kehäkulma.
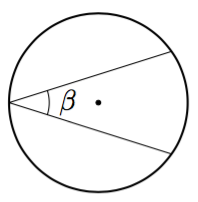
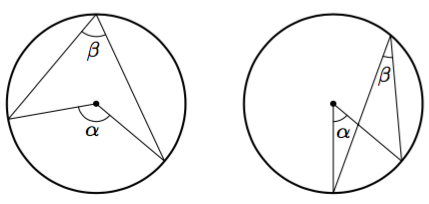
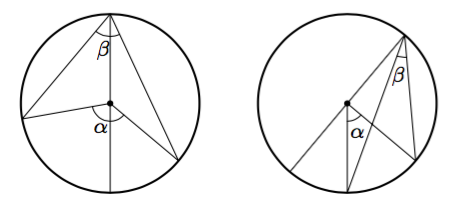
Edellisessä tehtävässä osoitettiin, että tietyssä tilanteessa keskuskulma on kaksi kertaa niin suuri kuin samaa kaarta vastaava kehäkulma. Toisin sanottuna kehäkulma on puolet samaa kaarta vastaavasta keskuskulmasta. Seuraavassa teoreemassa osoitetaan, että tämä on aina totta. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Kehäkulman suuruus on puolet samaa kaarta vastaavan keskuskulman suuruudesta.
Seuraavassa tehtävässä harjoitellaan kehäkulmalauseen soveltamista.
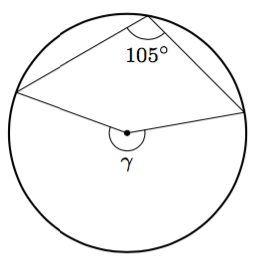
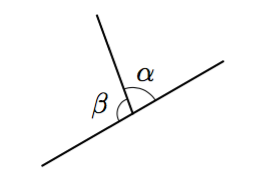
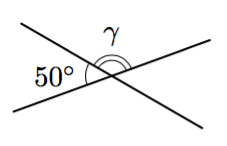
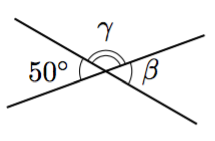
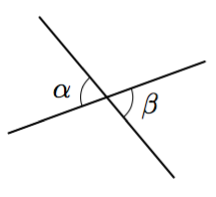
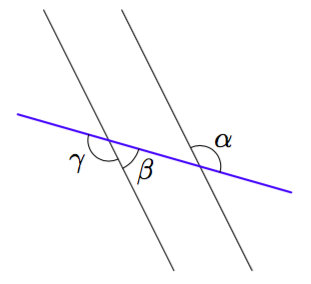
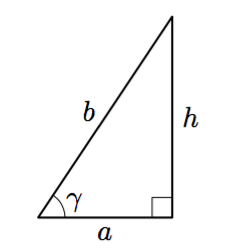
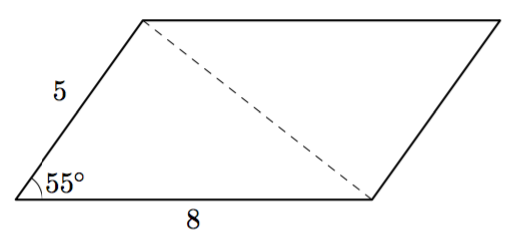
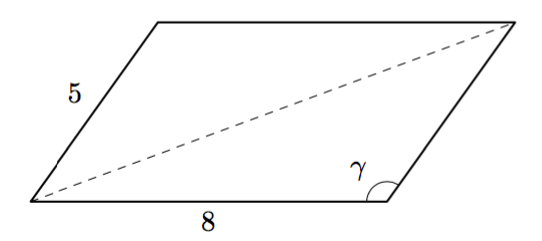
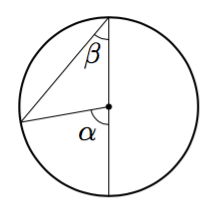
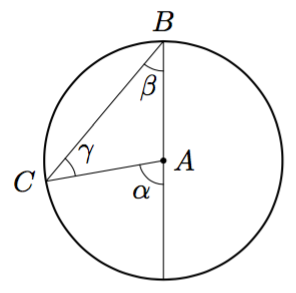
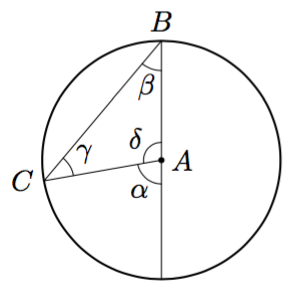
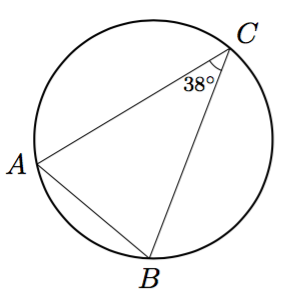
Päättele kulman $\gamma$ suuruus kehäkulmalauseen avulla.
-
-
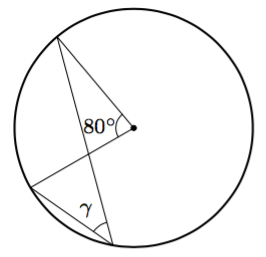
Seuraavissa tehtävissä tutkitaan erilaisia kehäkulmia kehäkulmalauseen avulla.
Tässä tehtävässä tutkitaan, mikä on puoliympyrään sisältyvän kehäkulman suuruus.
- Piirrä vihkoosi harpin avulla ympyrä. Piirrä ympyrälle halkaisija, jolloin syntyy kaksi puoliympyrää. Valitse toinen puoliympyröistä ja piirrä jokin sitä vastaava kehäkulma.
- Päättele puoliympyrän kaarta vastaavan keskuskulman suuruus. Mikä on sitä vastaavan kehäkulman suuruus?
Vinkki: Kehäkulmalause.
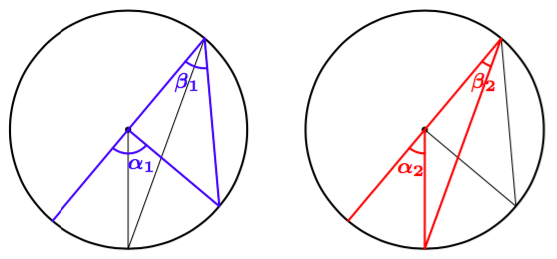
Tässä tehtävässä tutkitaan samaa kaarta vastaavien kehäkulmien suuruutta.
- Piirrä vihkoosi harpin avulla ympyrä. Valitse ympyrän kehältä pisteet $A$ ja $B$ ja niiden välisistä kaarista toinen. Piirrä jokin tätä kaarta vastaava kehäkulma. Anna sille nimeksi $\beta$.
- Piirrä jokin toinen samaa kaarta vastaava kehäkulma samaan kuvaan. Anna sille nimeksi $\gamma$.
- Piirrä vielä samaa kaarta vastaava keskuskulma. Anna sillekin nimi.
- Ilmaise kehäkulmat $\beta$ ja $\gamma$ keskuskulman avulla. Mitä havaitset?
Vinkki: Kehäkulmalause.
Tehtävien 2.32 ja 2.33 tuloksista saadaan seuraava teoreema:
TEOREEMA
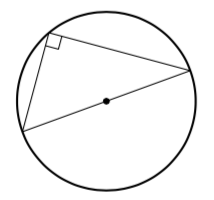
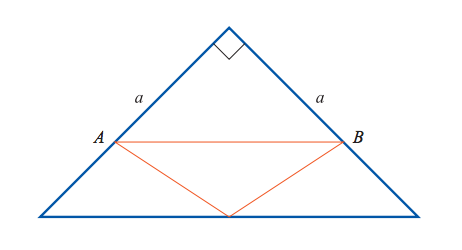
Puoliympyrän sisältämä kehäkulma on suora kulma.
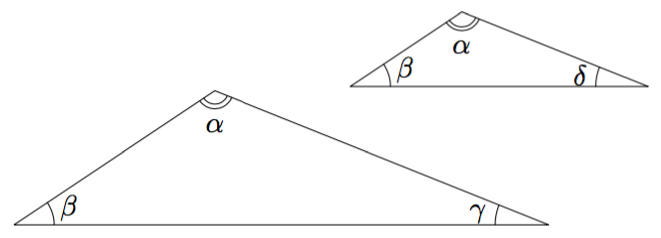
Samaa kaarta vastaavat kehäkulmat ovat yhtä suuret.
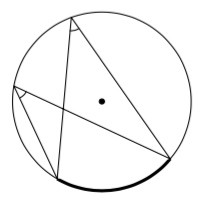
Perustelu: tehtävissä 2.32 & 2.33.

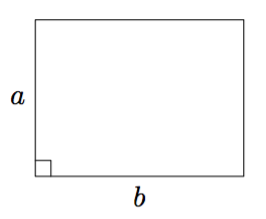
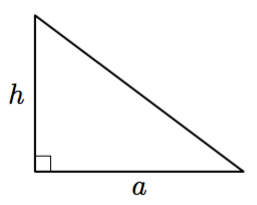
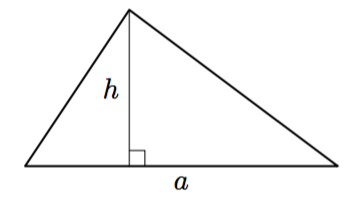




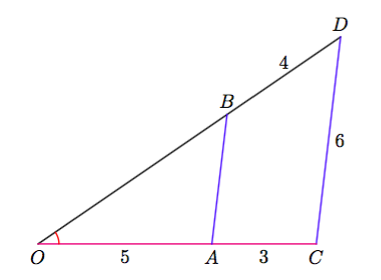
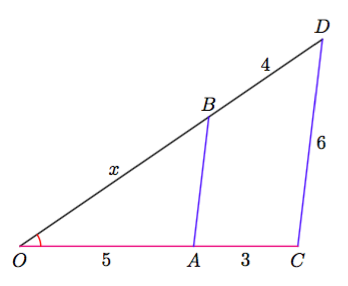
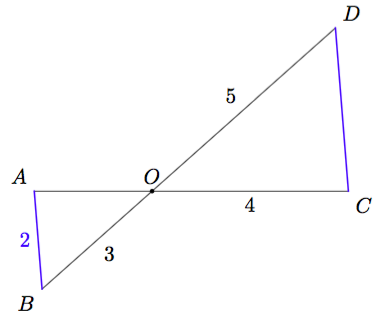







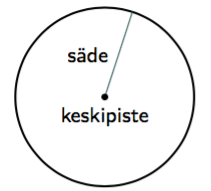
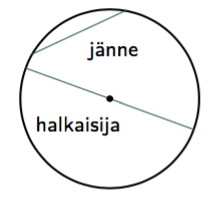



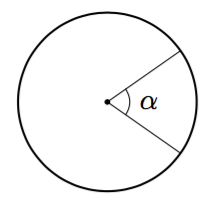








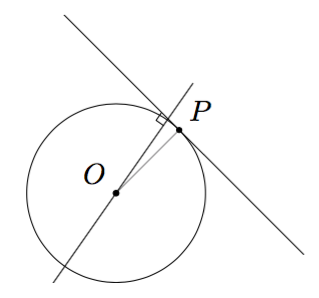




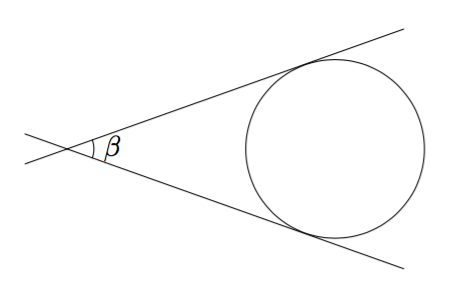

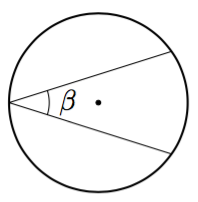
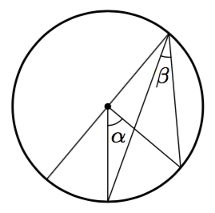






 Vinkki: teoreemat 17 sekä 4 tai 8.
Vinkki: teoreemat 17 sekä 4 tai 8. 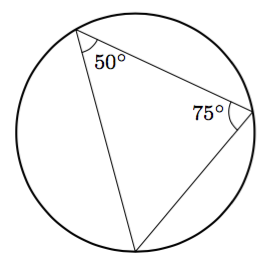
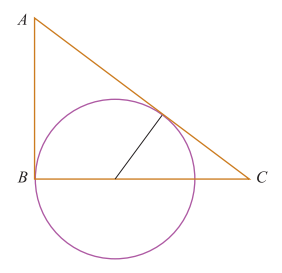
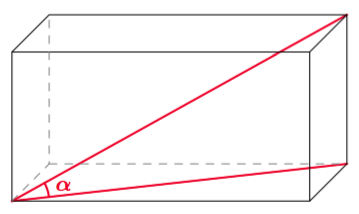
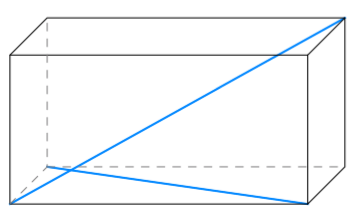
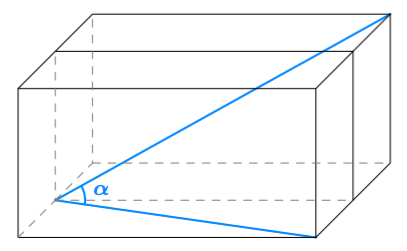
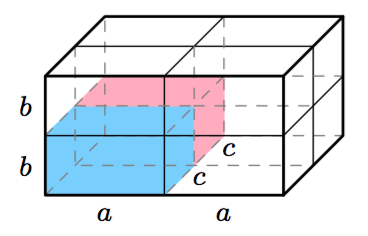
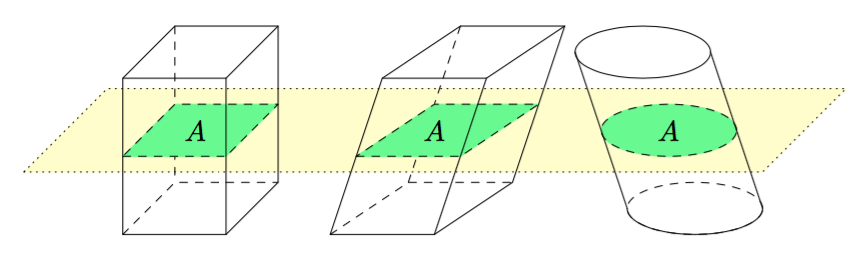
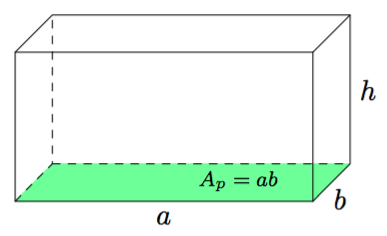
 Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä.
Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä. 
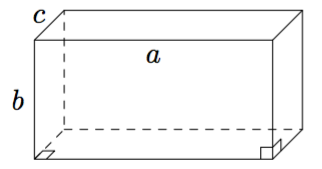
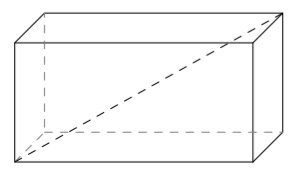
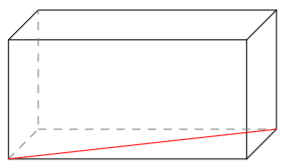
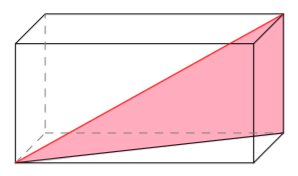
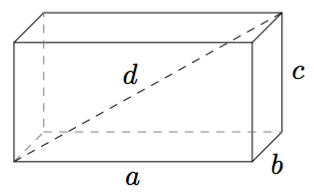

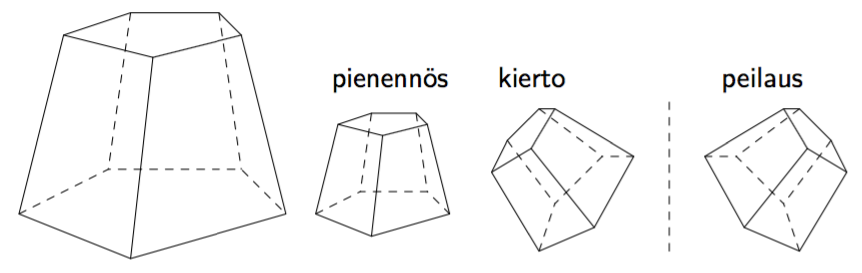
 (Yllä olevat punaiset kuvat Robert Webb,
(Yllä olevat punaiset kuvat Robert Webb,